La somma di molte variabili casuali uguali sappiamo che, all'aumentare del numero delle variabili e del numero delle prove, tende ad avere una distribuzione "gaussiana". Lo stesso accade se sommiamo molte variabili casuali diversamente distribuite. La precisazione e la dimostrazione di questo fatto può essere compresa solo in studi molto avanzati:  non c'è un confine alle conoscenze matematiche …
  

U = 0;
for(j in 1:7) U = U+rnd;
for(j in 1:8) U = U+rnd*rnd;
for(j in 1:6) U = U+sqrt(rnd);
for(j in 1:3) U = U+sin(rnd*3)
     Metto in U la somma Σi Ui di 24 variabili casuali numeriche indipendenti.  All'aumentare delle prove (100, 200, 400, 800, …, 12800) l'istogramma tende a stabilizzarsi su un andamento approssimativamente gaussiano. All'aumentare del numero delle variabili (comunque siano distribuite, a patto che non ve ne sia una che "prevarichi le altre") questa approssimazione migliora.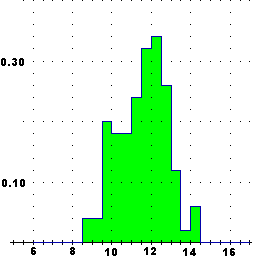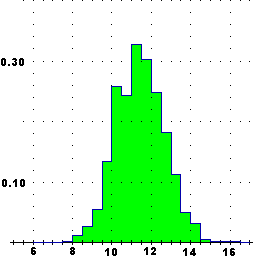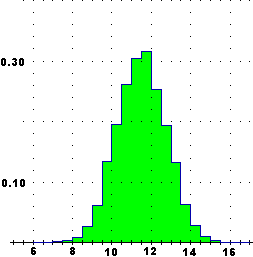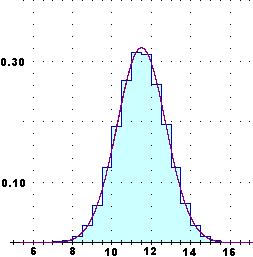